КОГЕРЕНТНОСТЬ  И  ВЫСОКОЭФФЕКТИВНОЕ  СЖИГАНИЕ 

ВЛАЖНОГО  БУРОГО  УГЛЯ

 

 

Известно, что реальная эффективность преобразования химической энергии топлива в процессе горения низка. Особенно это актуально при сжигании влажного бурого угля. Эффективность преобразования тепловой энергии в электроэнергию на теплоэлектростанциях не превышает 40%. А с учетом затрат энергии на добычу, переработку и доставку топлива потребителям, суммарный КПД тепловых установок может составить 10-15%.

Недостаток в технических решениях, позволяющих повысить эффективность производства электроэнергии из каменного и бурого угля безусловно отражается как на загрязнении атмосферы, так и на эффективном сбережении этих дорогих энергоносителей. В этой связи, представляется актуальным внедрение эффективных технологий сжигания угля, как одной из приоритетных задач теплоэнергетики.

Поскольку углеводородные топлива являются сложными химическими веществами, а пока процессы горения несовершенны, то в процессе их горения образуется целый “букет” других попутных веществ и токсичных газов, бесцельно уносящих неиспользованную внутреннюю энергию топлива в атмосферу.

  Горение-это одно из самых сложных известных человеку явлений. С научной точки зрения, горение - это цепная реакция последовательного дробления частиц топлива на все более мелкие заряженные радикалы, это и физико-химические процессы преобразования химической энергии межмолекулярных связей, это и физические процессы преобразования энергии на молекулярном и атомном уровнях, в тепло и свет, и многие другие процессы, протекающие одновременно.

Скорость реакции горения может быть найдена с помощью уравнения Аррениуса:

 

k = A ∙ e ^-Ea/RT

 

где A - постоянная, зависящая от природы реагирующих веществ; R - универсальная газовая постоянная [8,314 Дж/(моль ∙ К) = 0,082 л ∙ _═атм/(моль ∙ К)]; Ea - энергия активации.

Рассмотрим качественно, какова с позиции квантовой механики природа энергии активации в химической реакции, и чем определяется ее величина [1, 2]. Любая химическая реакция связана с перемещениями ядер атомов, из которых состоят молекулы реагентов, и с перестройкой их электронного окружения. Рассмотрение подавляющего большинства химических событий возможно на основе приближения Борна-Оппенгеймера. которое заключается в том, что вследствие малой массы электронов в сравнении с ядрами совокупность электронов в молекуле можно рассматривать как быструю подсистему. Это позволяет отдельно рассматривать и рассчитывать ядерное и электронное движения. Если ядра атомов находятся в некоторой конфигурации относительно друг друга, то электронное распределение приходит в соответствие с ядерной конфигурацией очень быстро, за время, за которое ядра практически не успевают переместиться. Быстрая электронная подсистема находится, таким образом, всегда в состоянии, которое определяется ядерной конфигурацией. Можно сказать, что электронное распределение отслеживает движения ядер и успевает подстроиться под них. С другой стороны, стационарное для данной ядерной конфигурации распределение электронной плотности определяет силы, действующие на ядра, и, таким образом, определяет их движение. Потенциальная энергия системы атомов определяется расположением электронов и ядер. Поскольку распределение электронов задано взаимным расположением ядер, то любому такому расположению соответствует единственное значение потенциальной энергии системы. Зависимость потенциальной энергии от ядерной конфигурации может быть выражена графически как поверхность потенциальной энергии (сокращенно ППЭ), Любой ядерной конфигурации будет соответствовать точка на поверхности потенциальной энергии.

Переход молекулы с одной поверхности потенциальной энергии на другую связан с изменением электронного и/или спинового состояния молекулы.

            В реакциях горения важное значение имеет не только молекулярная, но и спиновая динамика, играющая в элементарных химических актах двоякую роль. С одной стороны, она активно влияет на механизм и кинетику реакции. С другой стороны, спиновая динамика очень чутко реагирует на молекулярную динамику элементарного химического акта.

Из спиновой химии известно [3], что химическими реакциями управляют два фундаментальных фактора - энергия и спин. При этом запрет химических реакций по спину непреодолим. Если в химической реакции сталкивающиеся молекулы имеют антипараллельные спины (синглетное состояние), образование химической связи происходит. Если взаимодействующие молекулы имеют параллельные спины (триплетное состояние), то молекула может образоваться только в триплетном, возбужденном состоянии. Поскольку такие состояния обычно лежат высоко по энергии, в подавляющем большинстве случаев химические реакции в триплетной паре невозможны

Согласно правила Вигнера статистический вес встреч двух молекул в синглетном состоянии равен 1/4,  а статистический вес встреч в триплетном состоянии равен 3/4. В подавляющем  большинстве случаев основное состояние продуктов химической реакции является синглетным, и поэтому следует ожидать, что только четверть встреч реагирующих молекул могут дать продукт реакции. Такие процессы, как правило, протекает безактивационно, т.е. энергия активации реакции близка к нулю. Образующаяся молекула находится в основном электронном состоянии. Реакция протекает быстро и эффективно, если молекула имеет возможность отдать энергию, выделяющуюся при образовании связи, другим частицам или перераспределить ее между многими колебательными модами.

            К особенности спиновой динамики относится возможность когерентного контроля химических реакций [4, 5, 6]. В когерентных режимах можно ожидать увеличения выходов реакций, селективности процессов, самоочистки поверхностей от каталитических ядов и т.д. за счет увеличения статистического веса синглетных состояний встречающихся молекул до 1/2. И эти ожидания подтвердились, особенно в химических осцилляторах с вынужденными, принудительными осцилляциями .

Но прежде чем обсудить возможность такого контроля, кратко суммируем, что такое когерентность в квантовой механике. Рассмотрим некоторую молекулярную систему. Оператор энергии этой системы обозначим через Ή. Стационарные (собственные) состояния y_k и уровни энергии этих стационарных состояний E_k находятся из решения уравнения Шредингера

Ήy_k = E_k y_k

 

Согласно квантовой механике система может находиться в состоянии линейной суперпозиции стационарных состояний

 y = å c_k y_k

           ^k

Измеряемой величиной является квадрат модуля волновой функции

 

|y|² = å |c_k|² |y_k|²   +  åå c^*_n c_k y^*_ny_k

           ^{k                                 k   n}                                 

         Эта величина состоит из двух частей. Первое слагаемое в правой части отражает населенности |c_k|² стационарных состоянийy_k  в линейной суперпозиции. Очень интересным является второе слагаемое в правой части этого выражения. Оно показывает, что вклады разных стационарных состояний в наблюдаемую величину интерферируют. Это интерференционное слагаемое изменяется со временем согласно уравнению

 

|y(t) |² = å |c_k|² |y_k|²   +  åå c^*_n c_k y^*_ny_k exp [- (E_k - E_n)t / ћ]

                        ^{k                                   k  n}                                 

Видно, что именно за счет перекрестных произведений стационарных состояний интерфренционная картина изменяется со временем. Величины с_n*с_k (n ¹ k) характеризуют когерентность состояния квантовой системы.

Эти общеизвестные положения квантовой механики непосредственно проектируются на реагирующие системы. Обозначим через y_нач начальное состояние молекулярной системы (исходное состояние реагентов) и через y_кон конечное состояние молекулярной системы (состояние продуктов реакции). Следует ожидать, что при движении вдоль координаты реакции (от состояния реагентов к состоянию продуктов реакции) молекулярная система будет проходить через суперпозицию состояний y_нач и y_кон. А это означает, что при движении вдоль координаты реакции, т.е. в ходе элементарного акта химической реакции важную роль может играть квантовая когерентность.
                Чтобы пояснить возможность когерентного контроля химических реакций,  рассмотрим переход между двумя состояниями. Пусть в начальный момент времени, t = 0, система находится в состоянии 1 с энергией E₁, и пусть имеется состояние 2 с энергией E₂, равной E₁, т.е. E₂ = E₁. Предположим, что эти два состояния связаны некоторым взаимодействием с матричным элементом перехода, равным V. Обсудим вероятность p(t) найти систему в любой момент времени в состоянии 2. Временная зависимость этой вероятности очень сильно зависит от когерентности. Если переход из начального состояния 1 в конечное состояние 2 происходит некогерентным образом, то со временем происходит выравнивание населенностей этих состояний, и после достижения p = 1/2, населенности этих состояний в дальнейшем сохраняют значение 1/2. В случае когерентного движения искомая вероятность равна

 

              P = sin² (Vt / ћ).

 

Два обстоятельства в этом результате совершенно замечательные:

а) эта вероятность осциллирует, т.е. она не изменяется монотонно, как это ожидается для некогерентного движения;

б) эта вероятность в определенные моменты времени достигает значения 1.

Когда при Vt / ћ = p/4 эта вероятность становится равной 1/2, оба состояния оказываются равнозаселенными, переход из начального состояния в конечное продолжается как бы по инерции дальше, до полного перехода системы в состояние 2 и т.д. Этот пример показывает, что квантовая когерентность может играть очень важную роль в процессах переходов и в элементарных химических актах.

Как можно было бы реализовать то, что называется когерентным контролем реакции в данном примере? Предположим, что возбужденная молекула, из состояния 2, может, например, диссоциировать. Наибольший выход продуктов распада получится в том случае, когда в результате когерентного движения система полностью оказывается в состоянии 2, т.е. в момент времени, который удовлетворяет условию

 

Vt / ћ = 1/2 (2n + 1) π,    n =  0, 1, 2, …

 

Из этого примера видно, что можно оптимизировать химическое превращение, используя когерентный характер движения системы вдоль координаты реакции.

            На практике, спиновое когерентное состояние систем, участвующих в химических реакциях, может быть достигнуто путем использования спинорного поля, которое можно генерировать с помощью устройств, созданных на основе специально организованного ансамбля классических спинов, в котором реализуется максимальная энергия взаимодействия не только между соседними, но и удаленными спинами. Система взаимодействующих спинов является при этом своеобразным усилителем малых эффектов каждого отдельного спина.

Принципы построения реального генератора спинорного поля (СП) изложены в [7].

            Так как спин рассматривается нами как источник СП, то в соответствии с концепцией Р. Утиямы [8] объектом, чувствительным к воздействию  излучаемого генератором СП, должна быть спиновая система материальной среды. Причем в отношении величины эффекта, система спинов имеет преимущество перед индивидуальным спином микрочастицы. Сложная неравновесная спиновая структура, обладающая большим запасом квазивырожденных по энергии состояний,  может  выполнять  роль  системы,  в  которой  действие  СП может накапливаться (спиновое насыщение)  и приводить к заметным  макроскопическим  изменениям.

            Исследования влияния спинового когерентного состояния влажного бурого угля на эффективность его сжигания проводились с использованием калориметра KL-10.

            Идеология исследований заключалась в том, что при увеличении скорости горения угля, вызванное его спиновым когерентным состоянием, в первую минуту после зажигания угля  вода в калориметре должна быстрее нагреваться. На рис. 1 представлена схема эксперимента.

 

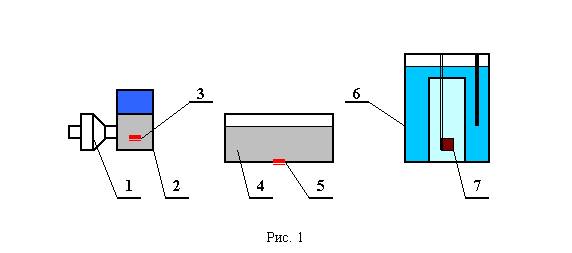
1 - генератор спинорного поля, 2 – резонатор спиновых состояний, 3 - чип-транслятор,   4 – емкость с бурым углем,  5 – чип-индуктор , 6 – калориметр KL-10, 7 – навеска угля

 

            В емкости с бурым углем 4 помещался сип-индуктор 5, который по каналу квантовой связи, создаваемому с использованием физики запутанных квантовых состояний (the physics of entangled quantum states), связан с чип-транслятором 3. Чип-транслятор размещался в резонаторе спиновых состояний  2, к которому подключен генератор СП 1 . 

В калориметр 6 помещались навески исследуемого бурого угля 7 весом 1 г, при различных влажностях. Давление кислорода в калориметре 28 ати.

После включения генератора СП 1 происходило возбуждение резонатора спиновых состояний 2 до требуемого уровня. Одновременно с возбуждением резонатора происходило возбуждение чип-транслятора 3, который за счет эффекта запутанных квантовых  состояний осуществлял трансляцию спинового возбуждения на чип-индуктор 5. Чип-индуктор производил спиновую накачку бурого угля 4 и переводил его в беспрерывно удерживаемое спиновое когерентное состояние.

            Исследования проводились на бурых углях доставленных из Германии и Польши, влажностью 8, 12, 15 и 20%. Перед сжиганием уголь измельчался до фракции 0,6 – 0,8 мм.

            Количество сжиганий – по три на одно значение влажности.

            С использование статистических данных результатов исследований построены графические зависимости изменения температуры воды в калориметре через 1 минуту после сжигания угля (рис. 2 и 3).

 

 

 

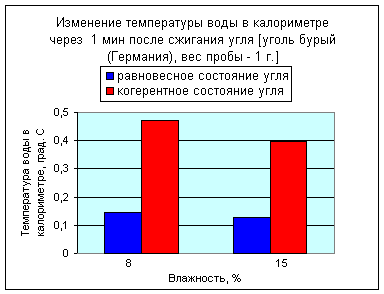
Рис. 2

 

 

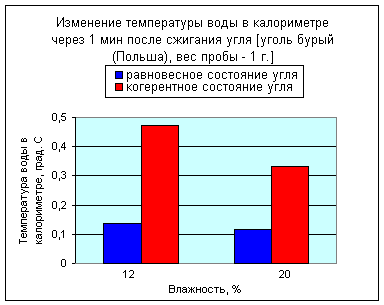
Рис. 3

 

Во всех случаях сжигание угля в когерентном состоянии происходило со взрывом.

 

            Экспериментальная проверка результатов исследований в производственных условиях проводилось в условиях городской котельн1ой оборудованной четырьмя котлами мощностью 12 Мдж каждый. В котлах сжигается каменный уголь калорийностью 4900-5400 ккал/кг, зольность 10-15%, влажность 12-18%. Содержание несгоревшего угля в золе – 18-22%. Схема эксперимента приведена на рис. 4.

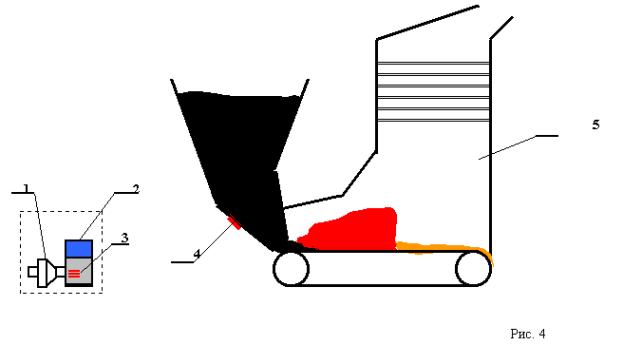
1 - генератор спинорного поля, 2 – резонатор спиновых состояний, 3 - чип-транслятор, 4 – чип-индуктор,  5 –  котел

 

 

            К бункеру с углем котла  5 был прикреплен чип-индуктор 4, с который по квантовому каналу связан с чип-транслятором 3. Чип-транслятор размещался в резонаторе спиновых состояний  2, к которому подключен генератор СП 1 .

После включения генератора СП 1 происходило возбуждение резонатора спиновых состояний 2 до требуемого уровня. Одновременно с возбуждением резонатора происходило возбуждение чип-транслятора 3, который за счет эффекта запутанных квантовых  состояний осуществлял трансляцию спинового возбуждения на чип-индуктор 4. Чип-индуктор производил спиновую накачку угля в бункере котла 4 и переводил его в беспрерывно удерживаемое спиновое когерентное состояние.

            В результате проведенных экспериментов установлено снижение содержания несгоревшего угля в золе с 18 - 22% до 8 – 11%.

 

            На основании проведенных исследований можно сделать следующие выводы:

1. Перевод угля в спиновое когерентное состояние обусловливает увеличение скорости его горения ~ в 2 раза .

2. С целью повышения эффективности сжигания угля на тепловых электростанциях и котельных можно рекомендовать использование технологии перевода угля в спиновое когерентное состояние.

 

 

ЛИТЕРАТУРА

 

1.       Бучаченко АЛ., Салихов К.М., Молин Ю.Н., Сагдеев Р.З. Магнитные и спиновые эффекты в химических реакциях. Новосибирск: Наука, 1978.

2.       Buchachenko A.L., Frankevich E.L. Chemical generation and reception of microvawes. N.Y., 1994.

3.       Бучаченко АЛ. Химия на рубеже веков: свершения и прогнозы // Успехи химии. 1999. Т. 68. С. 85-102.

4.       G. Kothe, M. Bechtold, G. Link, E. Ohmes, J. -U. Weidner Chem Phys Lett, 283, 51 (1998).

5.       W. Hohmann, D. Lebender, J. Muller, N. Schinor, F. Schneider J.Phys Chem A, 101,9132(1997).

6.       S. Jakubith, H. H. Rotermund, W.Engel, A. von Oertzen, G. Ertl. Phys. Rev. Lett, 65, 3013(1990).

7.       Краснобрыжев В.Г. Спинорные поля и их генерация. http://entron.narod.ru/.

8.      Утияма Р. К чему пришла физика. (От теории относительности к теории калибровочных полей). М., Знание, 1986, 224 с.

 

 

В. Краснобрыжев, Г.Пацоха

E-mail: entron@rambler.ru

Тел. (38044) 475-96-75